Una distinción de particular importancia es aquella entre variables dependientes e independientes. Los términos “dependiente” e “independiente” se utilizan para representar una relación de “causalidad” entre dos variables. La relación es la siguiente: el valor de la variable dependiente ‘depende’ del valor de la variable independiente. Es decir, la variable independiente determina el valor de la variable dependiente. Utilizando otros términos, la variable independiente “causa” la variable dependiente.

Por ejemplo: Un buen maestro causa que los estudiantes aprendan. En este caso, “buen maestro” es la variable independiente, mientras que “grado de aprendizaje” (de los estudiantes) es la variable dependiente.

Sin embargo, no siempre es fácil, saber cuál es la variable dependiente y cuál la independiente en una relación. De acuerdo con el ejemplo previo, ¿el hecho de que los estudiantes de la escuela A tengan un mejor rendimiento que los de la escuela B significa que los maestros de la escuela A son mejores que los de la escuela B?

El problema de la determinación de causalidad es uno de los problemas más serios que enfrenta la estadística. El análisis empírico o estadístico sólo puede decirnos si dos variables parecen estar relacionadas, pero no puede decirnos:

a Si de hecho existe una relación de dependencia

b cuál es la dirección de dicha relación (cuál es la “causa” y cuál el efecto o la variable “causada”).

Una “teoría” es necesaria para dar plausibilidad a una relación empírica

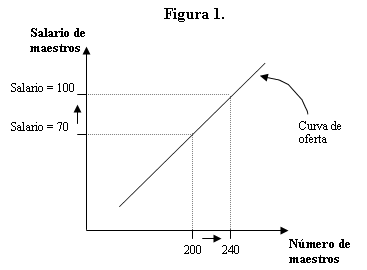
Vayamos por un momento al tema de la interpretación de gráficos (tratado en mayor detalle en los módulos 3 y 4 de esta guía). Un gráfico representa una relación entre por lo menos dos variables. En matemáticas y geometría, la variable dependiente se denomina X y se representa en el eje horizontal del gráfico, mientras que la variable independiente se llama Y (o ‘independiente’, para facilitar la memorización) y se representa en el eje vertical. En la Figura 1, a continuación, se muestra un ejemplo de una “curva de oferta” que presenta la relación entre dos variables: el salario de los maestros y la cantidad o número de maestros disponibles o que ofrecen sus servicios.