(3) Cuando se describen distribuciones asimétricas (sesgadas) positivas o negativas, la media no es la mejor medida de tendencia central disponible. Mientras mayor sea la asimetría o sesgo de los datos, mayor utilidad tendrá la mediana (y más engañosa será la media), porque la mediana estará más cerca del ‘valor promedio’ real de las observaciones. Por ejemplo, en el caso de una distribución asimétrica positiva, la media se encuentra ‘inflada’ por la minoría de las observaciones que tienen un valor mayor. Esto sucede, por ejemplo, con el ingreso per cápita, puesto que las distribuciones del ingreso son asimétricas positivas. En las siguientes figuras se muestran las posiciones relativas de la media, la moda y la mediana en cuatro distribuciones asimétricas.

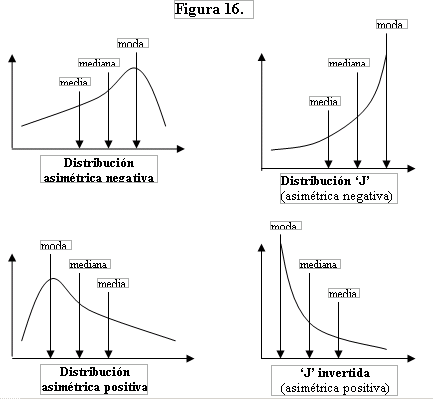
Observe que cuando la distribución es asimétrica ‘positiva’, (es decir, el extremo más largo de la distribución apunta hacia el este o hacia su derecha), la moda está a la izquierda de la mediana, y a su vez, la mediana está a la izquierda del promedio. Sucede lo contrario cuando la distribución es asimétrica negativa o sesgada negativamente. Esto nos lleva a una consideración final: si una distribución es asimétrica, es decir, notoriamente sesgada, la mediana será mejor que la media (promedio aritmético) para describir la tendencia central de la distribución de los datos. Observe las figuras anteriores. Note que en todas las distribuciones asimétricas, la mediana efectivamente se acerca más que la media al valor ‘promedio o ‘normal’ de las observaciones o, en otras palabras, refleja mejor la existencia de un sesgo en los datos.