Las ventajas y limitaciones de usar la media, la moda y la mediana para describir un conjunto de datos depende estrictamente del tipo de la distribución de datos. En general, se prefiere la media para describir la tendencia central, aunque algunas distribuciones se describen mejor por medio de la moda y la mediana. A continuación, se evaluarán la aplicabilidad de estos tres ‘promedios’ a diferentes tipos de distribuciones.

(1) En una distribución normal, la media, moda y mediana tienen un valor idéntico (Figura 15). Esto en realidad es evidente, dado que una distribución normal es perfectamente simétrica, y la curva tiene un sólo punto máximo (moda) que también se encuentra en el centro. Así, la media debe ser nuestra medida preferida de tendencia central para los conjuntos de datos que se distribuyen normalmente, puesto que es más fácil de calcular y de usar en forma matemática.

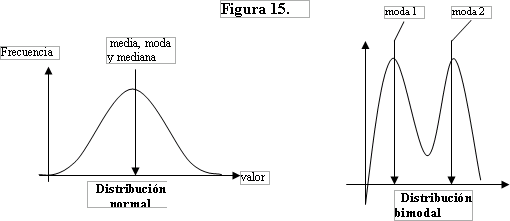
(2) Una distribución bimodal tiene dos puntos máximos (Figura 15). Esto hace que la media y la mediana no sean de utilidad, puesto que sus valores estarán en algún lugar entre los dos puntos máximos y distorsionarán enormemente la descripción de la distribución. En este caso hay dos modas. Sin embargo, una distribución bimodal es poco común y en general podemos decir que consta de dos distribuciones que se pueden analizar en forma independiente.