La figura 17-b (abajo) provee otro buen ejemplo de la importancia de las medidas de dispersión cuando queremos describir distribuciones. Observe que el ejemplo es difiere del anterior en que las medidas de tendencia central (media, mediana y moda) son ahora distintas en las dos distribuciones (curvas I y II) de la figura, y mayores en valor en todos los casos para la distribución II. La distribución I muestra una situación en la que la mayoría de los estudiantes de un país se concentran alrededor del valor X, cuando se la compara con la distribución II, donde la dispersión del nivel de conocimientos entre los estudiantes del país es mucho mayor.
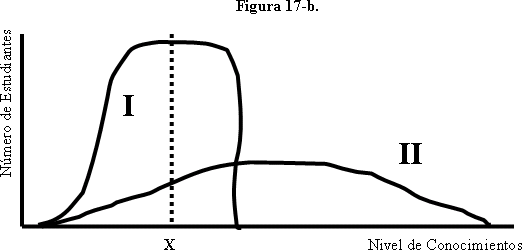
Finalmente, observe que, en la Figura 17-b, el país I presenta una menor dispersión y por lo tanto un mayor grado de equidad relativa en la distribución del nivel de conocimientos. Pero, al mismo tiempo, en el país I al menos la mitad de los estudiantes tiene un nivel de conocimientos inferiores a X, mientras que en el país II la gran mayoría de los estudiantes (más del 80%) tienen un nivel de conocimientos superiores a X. En términos técnicos, esto significa que el grado de equidad absoluta de la distribución de conocimientos en el país II es superior a la del país I, si consideramos X como un estándar mínimo en el nivel de conocimientos deseado. Esta información es importante para la toma de decisiones de política educativa.
Como ya se mencionó, los descriptores o indicadores de dispersión o variabilidad más comunes son la desviación estándar y la varianza. A continuación explicaremos estos dos importantísimos indicadores, los cuales se usan en forma generalizada en investigación en ciencias sociales, incluida la investigación sobre educación.