Las distribuciones de frecuencias continuas representan los diferentes valores y su frecuencia en un continuo. Se podría decir que es equivalente al uso del gráfico de barras para las variables discretas, sólo que, en este caso, el “gráfico de barras” es “continuo”. Por ejemplo, el Punto M de la Figura 12 indica que 2600 estudiantes obtuvieron una calificación de 55. El gráfico también expresa que la calificación 25 fue también obtenida por 2600 estudiantes.

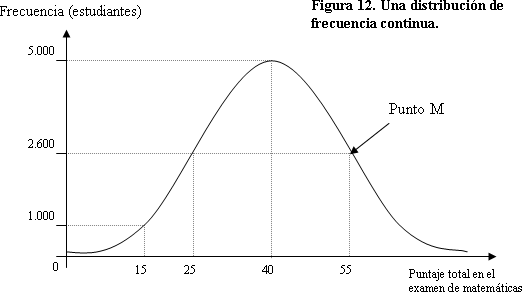
La Figura 12 representa una distribución de frecuencia continua de las calificaciones en los exámenes de admisión a la universidad en el país de ‘Normalia’. La gráfica indica, que 5000 estudiantes obtuvieron una calificación de 40 puntos, mientras que sólo 2600 estudiantes obtuvieron una calificación de 25 puntos. También indica que 40 fue la calificación promedio de todos los estudiantes que dieron la prueba. Este tipo de distribución, simétrica y con forma de ‘campana’, es conocida con el nombre de distribución normal.

Las distribuciones de frecuencia continuas también entregan información acerca de las “distribuciones relativas”. Para comenzar, el área total bajo la curva de una distribución continua representa el 100% de las observaciones. En el análisis matemático, las áreas bajo una curva se calculan usando integrales. Los estadísticos han ideado formas más eficaces de analizar las distribuciones continuas: han creado una serie de distribuciones ‘tipo’ o ‘ideales’ (como por ejemplo la distribución normal), cada una de las cuales tiene ciertas características predeterminadas que permiten una descripción estadística rápida muy sofisticada (con la ayuda de ‘tablas estadísticas’).