Tema 4. Transferencia del aprendizaje matemático a situaciones del mundo real y auto reflexión del aprendizaje
Tema 3. Aplicación del razonamiento matemático en la resolución de problemas cotidianos

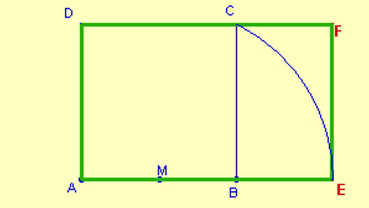
El rectángulo áureo
Un rectángulo cuyos lados están en una proporción igual a la razón áurea es llamado un rectángulo áureo. Este es un rectángulo muy especial como veremos. Los griegos lo consideraban de particular belleza y lo utilizaron asiduamente en su arquitectura.
Al parecer a la mayoría de las personas también les parece más agradable a la vista un rectángulo con esas proporciones entre sus lados, inconscientemente se diseñan infinidad de cosas que resultan tener la forma de un rectángulo áureo: las hojas de papel tamaño carta miden 11 x 8 pulgadas, por ejemplo; esto nos da la proporción 1.37 que se parece a la razón aurea.
Para construirlo a partir de un cuadrado de lado AB basta con determinar el punto medio M de uno de los lados (AB), y trazar con centro en el punto M, una circunferencia que pase por uno de los vértices (C) del lado opuesto.

• o Rectángulo raíz de 2: Se denomina así al rectángulo en el que la relación entre base y altura es igual a la raíz cuadrada de dos. Si b y h son los lados, b/h= . El interés de este rectángulo radica en que si es dividido en dos mitades por su lado más largo, los dos nuevos rectángulos obtenidos tiene cada uno la mitad de área que el original, pero exactamente sus mismas proporciones. Es por ello que es el formato utilizado para la normalización de folios de papel según la norma DIN, entre otros usos.
• Construcción partiendo del cuadrado: De forma similar al rectángulo áureo, se traza con centro en el punto A, una circunferencia que pase por el vértice opuesto C


 

El número áureo, también denominado “número de oro”, divina proporcion “número dorado”, “sección áurea”, “razón áurea”, “razón dorada”, “media áurea”, “proporción áurea”, “divina proporción”, representado por la letra griega Φ (fi) (en honor al escultor griego Fidias), es el número irracional:



Sección áurea obtenida en una espiral logarítmica.

Se trata de un número que posee muchas propiedades interesantes y que fue descubierto en la antigüedad, no como “unidad” sino como relación o proporción. Esta proporción se encuentra tanto en algunas figuras geométricas como en las partes de un cuerpo, y en la naturaleza como relación entre cuerpos, en la morfología de diversos elementos tales como caracolas, nervaduras de las hojas de algunos árboles, el grosor de las ramas, proporciones humanas, etc.



Rectángulos áureos en el Partenón



Rectángulos áureos en la Mona Lisa de Da Vinci.



Razón áurea en la concha del Nautilus

1. Según el propio Leonardo de Pisa, Fibonacci en su Libro de los ábacos, la secuencia puede ayudar a calcular casi perfectamente el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos se empiezan a reproducir cuando tienen dos meses de edad).
2. La relación entre la cantidad de abejas macho y abejas hembra en un panal.
3. La relación entre la distancia entre las espiras del interior espiralado de cualquier caracol (no sólo del nautilos)
4. La relación entre los lados de un pentáculo.
5. La disposición de los pétalos de las flores (el papel del número áureo en la botánica recibe el nombre de Ley de Ludwig).
6. La distribución de las hojas en un tallo
7. La relación entre las nervaduras de las hojas de los árboles
8. La relación entre el grosor de las ramas principales y el tronco, o entre las ramas principales y las secundarias (el grosor de una equivale a Φ tomando como unidad la rama superior).
9. La distancia entre las espirales de una piña.
10. La Anatomía de los humanos se basa en una relación Phi exacta, así vemos que:
1. La relación entre la altura de un ser humano y la altura de su ombligo.
2. La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.
3. La relación entre la altura de la cadera y la altura de la rodilla.
4. La relación entre el primer hueso de los dedos (metacarpiano) y la primera falange, o entre la primera y la segunda, o entre la segunda y la tercera, si dividimos todo es phi.
5. La relación entre el diámetro de la boca y el de la nariz
6. Es phi la relación entre el diámetro externo de los ojos y la línea inter-pupilar
7. Cuando la tráquea se divide en sus bronquios si medimos el diámetro de los bronquios por el de la tráquea se obtiene phi, o el de la aorta con sus dos ramas terminales (ilíacas primitivas), la anatomía esta llena de números phi en los órganos
8.  
9. No solo eso, esta comprobado que la mayor cantidad de números phi en el cuerpo y el rostro hacen que la mayoría de las personas reconozcan a esos individuos como LINDOS, BELLOS y PROPORCIONADOS. Si medimos los números phi de una población determinada y la comparamos con una población de modelos publicitarios, estos últimos resultan acercarse mas al número phi