
Existen algunos conceptos de básicos
de álgebra que es importante
considerar para el cálculo del
trinomio cuadrático general.
|
|
Es una expresión algebraica
que consiste en un número,
una variable o un producto
de una constante y una o más
variables. |
|
|
Es
un número o una letra
o varios números y
letras combinados entre si
mediante operaciones de multiplicación
y/o división. |
|
|
Es
una expresión algebraica
que consta de tres términos. |
|
|
Es
una expresión algebraica
que consta de dos o más
términos. |
|
|
Es
una expresión algebraica
que consta de tres términos
y cuyo mayor exponente es
2, (también se llama
trinomio de segundo grado). |
|
|
Es
aquel trinomio de segundo
grado que al factorizarse
da dos binomios exactamente
iguales (binomios al cuadrado). |
|
|
Es
aquel que al factorizarse
da dos binomios diferentes.
|
|
Un concepto que se debe conocer para
la determinación del trinomio
cuadrático general es la
factorización.
Factorización
Factorizar un número sobre un
conjunto dado, es descomponerlo en todos
los factores que lo forman. Por ejemplo:
Factores de -21 = ( -1 ) ( 21
) = ( -3 ) ( 7 ) = ( 3 ) ( -7 )
Factores de 21 = ( 1 ) ( 21 )
= ( -1 ) ( -21 ) = ( 3 ) ( 7 ) = ( -3
) ( -7 )
Factores de a2 - b = a ( a -
b )
Un número cuyos único
factores son el mismo número
y 1 se dice que es un número
primo. Por ejemplo:
Ejemplo
Instrucciones: calcular
el trinomio cuadrático general
que se pide.
El inciso que contiene los factores
de 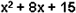 :
: