
Una estrategia que nos permite calcular
la raíz cuadrada de un número,
sin tener que desarrollar el algoritmo
de la operación, consiste en
conocer la raíz cuadrada de ciertos
números clave, el cuadrado de
los números dígitos y
el procedimiento seguido en la estimación
de resultados posibles.
|
Raíces
de números clave
|
Cuadrado
de números dígitos
|
|
|
|
|
|
1)
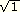
|
1
|
7)
0
|
0
|
2)
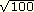
|
10
|
8)
1
|
1
|
3)
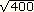
|
20
|
9)
2
|
4
|
4)
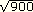
|
30
|
10)
3
|
9
|
5)
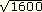
|
40
|
11)
4
|
16
|
6)
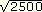
|
50
|
12)
5
|
25
|
|
|
|
13)
6
|
36
|
|
|
|
14)
7
|
49
|
|
|
|
15)
8
|
64
|
|
|
|
16)
9
|
81
|
|
Por ejemplo, para calcular la raíz
cuadrada de 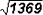
el procedimiento sería el siguiente:
1. Por 4) y 5)
se estima que el resultado debe estar
entre 30 y 40, con ello ya se conoce
que es un número de dos dígitos.
Por tanto el dígito de las decenas
= 3
2. Falta el dígito
de las unidades y por 10) y 14),
ese dígito puede ser 3 ó
7, ya que 3 (3) = 9 y 7 (7) = 49. Por
estimación, sí el dígito
de las unidades fuera 3 el número
1369 estaría más cerca
de 900 y si fuera 7, estaría
más cerca de 1600.
3. Se comprueba la cercanía
de ambos:
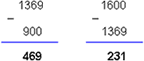
4. Por lo tanto, se prueba con 7 y
el número podría ser 37.
Prueba:

Cuando se trata de calcular la raíz
cuadrada de números cuyo dígito
de las unidades es 5, sólo basta
con calcular el primer paso ya que el
dígito de las unidades deberá
ser forzosamente 5.
Ejemplo
Instrucciones: obtener
la raíz cuadrada correspondiente.
Selecciona el inciso que tiene la respuesta
a 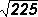 es:
es:
a) 25
b) 35
c) 5
d) 15
|